Karekök Hesaplama
Burada sayıların karekökünü hesaplayabilirsiniz.
Sayıyı aşağıdaki metin kutusuna girdikten sonra "Hesapla" tuşunu tıklayın. Aşağıda karekök ile ilgili
bazı bilgilere ulaşabilir, elle karekök hesaplayabilirsiniz.
Karekök nedir?
Bir sayının kendisi ile çarpımına sayının karesi denir. Bu işlemin tersi karekökdür. Yani karekök, bir sayının hangi sayının kendisi ile çarpımından elde edildiğini bulma işlemidir.
Örneğin:
2 x 2 işleminin sonucu 4'dür. Yani, 2'nin karesi 4'tür.
Bu durumda 4'ün karekökü 2'dir. Yani 4 sayısı 2 sayısının kendisi ile çarpımıyla hesaplanmıştır.
Karekök nasıl bulunur?
Karekök hesaplamak için hesap makinelerinden veya bu sayfadaki gibi bir hesaplayıcıdan yararlanırız. Ancak elle hesaplamak gerekirse aşağıdaki yöntemleri kullanabiliriz.
Karekök nasıl bulunur?
Karekök hesaplamak için hesap makinelerinden veya bu sayfadaki gibi bir hesaplayıcıdan yararlanırız. Ancak elle hesaplamak gerekirse aşağıdaki yöntemleri kullanabiliriz.
Asal Çarpanlarına Ayırarak Karekök Hesaplama
Bu yöntemde karekökü hesaplanacak sayıyı asal çarpanlarına ayırırız. Örneğin;
√400
= √2 x 2 x 2 x 2 x 5 x 5
= √24 x 52
= √16 x 25
= √16 x √25
= 4 x 5 = 20
Eğer sayıyı asal çarpanlarına ayırdığımızda karekökü tam olan sayılar ortaya çıkmıyorsa, karekökü tam olanları kökün dışına çıkarır,
kalan sayıyı yanına kök içinde yazarız. Örneğin:
√50
= √2 x 52
= √2 x 52
= 5√2
Bu ifade, 5 ile 2'nin karekökünün çarpılacağı anlamına gelir.
Kalanlı Bölme Yöntemi ile Karekök Hesaplama
Bunun için sayıyı sağdan sola doğru ikili parçalara ayırın.
Eğer ondalık kısım varsa burayı soldan sağa doğru ikili parçalara ayırın.
Ondalık sayılarda sonda tek sayı kalırsa yanına bir tane sıfır yazın.
Tamsayı için örnek:
Sayı = 12345
Ayrılmış sayılar:
1 23 45
Ondalık kısmı olan sayı için örnek:
Sayı = 12345,345
Ayrılmış sayılar:
1 23 45 , 34 50
535 sayısının karekökünü kalanlı bölme yöntemiyle hesaplayalım.
-
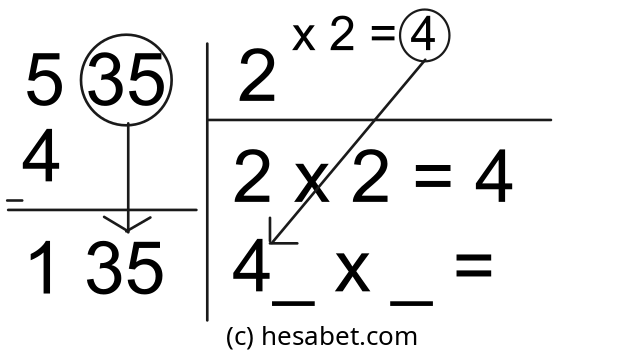
535 sayısını 5 35 şeklinde ayırın ve şekildeki gibi yazın.

-
Birinci gruptaki sayıya (5 sayısı) en yakın tam karekökü olan sayıyı bulun (4 sayısı),
kökünü (2 sayısı) bölen kısmına ve bölüm kısmına kare hesaplama işlemini (2x2=4) ve
bulunan kareyi birinci grubun altına yazın. Sonra birinci gruptaki sayıdan bu sayıyı
çıkarın(5-4=1).

-
İkinci grubu (Üstteki 5 35 yazan yerdeki 35 sayısını) 1'in yanına yazın. Buradaki sayı 135 olur. Bölendeki sayıyı (2), 2 ile çarpın ve sonucu bölüm
kısmına yanına _ x _ = ekleyerek yazın (4 _ x _ =)
-
_ olan yerlere aynı sayıyı yazacağız.
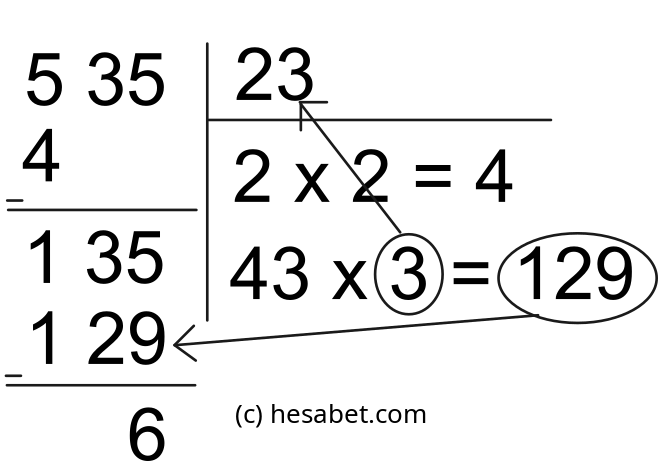
Çıkarmadan kalan 1 ve yukarıdan indirdiğimiz ikinci grup sayıyı (35) ekleyerek
oluşturduğumuz 135 sayısına en yakın sayıyı bulmak için _ olan yerlere hangi sayıyı yazmalıyız?
Örneğin 4 sayısını yazarsak çarpım 44 x 4 = 176 olur. Bu sayı 135 sayısından büyüktür.
Ama sayıyı 3 kabul edersek çarpım 43 x 3 = 129 olur ve bu sayı 135 sayısından küçüktür.
3 sayısını kullanacağız. Çarpımı (129'u) 135'in altına yazacağız. Bulduğumuz 3 sayısını da bölen kısmına
ekleyeceğiz (bölen kısmı 23 olacak). Önceki işlemde 5'den 4'ü çıkardığımız gibi şimdi de 135'den
129'u çıkarıp sonucu (6) alta yazacağız.
-
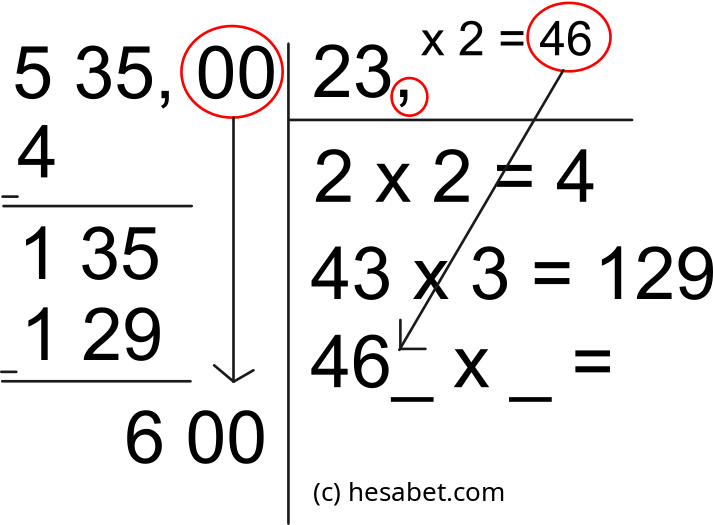
Şimdi yukarıdan indireceğimiz tamsayı veya ondalık sayı kalmadı. 6'nın yanına 00 yazıyoruz.
Eğer ondalık hanelerimiz olsaydı 2 tanesini buraya yazacaktık.
Ondalık kısmına geçtiğimizden bölendeki sayının yanına virgül ekliyoruz.
Bölen kısmındaki sayıyı (23) 2 ile çarpıp, öncekinde olduğu gibi bölüm kısmına
_ x _ = ekleyerek yazıyoruz (46_ x _ =).
-
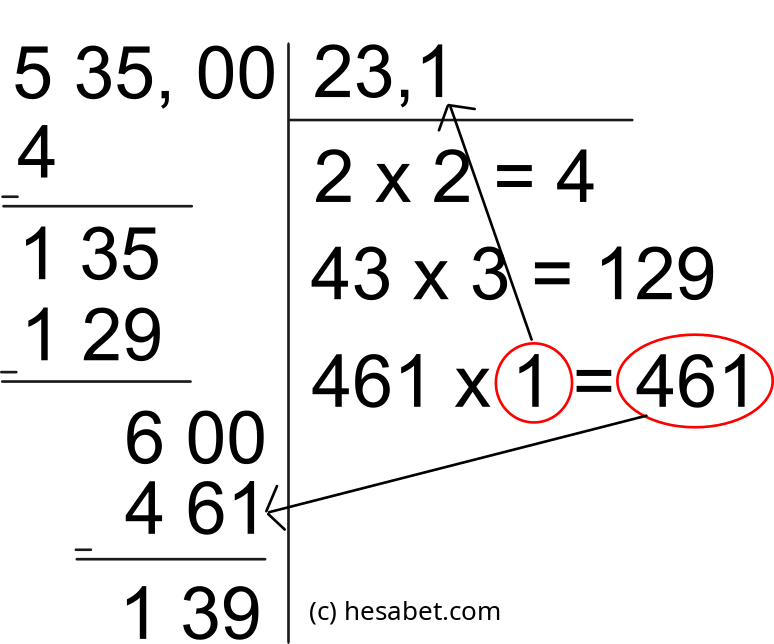
Şimdi öncekinde olduğu gibi _ olan yere hangi sayıyı yazdığımızda soldaki sayıya
(şu anda 6 ve 00 ile beraber 600 sayısı) en yakın sayıyı buluruz. Bunu hesaplıyoruz.
Bu sayı 1'dir. İşlem 461x1=461 olur. 1'i yukarıya,
461'i ise 600'ün altına yazıyoruz ve yine çıkarma işlemi yapıyoruz.
-
Buraya kadar yaptığımız işlemlerle karekökü 23,1 bulduk.
İşlemlere bu şekilde devam ederek dilediğimiz kadar ilerliyoruz.
1'den 100'e Kadar Sayıların Kareleri (© hesabet.com)
| Sayı | Karesi |
|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
| 21 | 441 |
| 22 | 484 |
| 23 | 529 |
| 24 | 576 |
| 25 | 625 |
| 26 | 676 |
| 27 | 729 |
| 28 | 784 |
| 29 | 841 |
| 30 | 900 |
| 31 | 961 |
| 32 | 1024 |
| 33 | 1089 |
| 34 | 1156 |
| 35 | 1225 |
| 36 | 1296 |
| 37 | 1369 |
| 38 | 1444 |
| 39 | 1521 |
| 40 | 1600 |
| 41 | 1681 |
| 42 | 1764 |
| 43 | 1849 |
| 44 | 1936 |
| 45 | 2025 |
| 46 | 2116 |
| 47 | 2209 |
| 48 | 2304 |
| 49 | 2401 |
| 50 | 2500 |
| 51 | 2601 |
| 52 | 2704 |
| 53 | 2809 |
| 54 | 2916 |
| 55 | 3025 |
| 56 | 3136 |
| 57 | 3249 |
| 58 | 3364 |
| 59 | 3481 |
| 60 | 3600 |
| 61 | 3721 |
| 62 | 3844 |
| 63 | 3969 |
| 64 | 4096 |
| 65 | 4225 |
| 66 | 4356 |
| 67 | 4489 |
| 68 | 4624 |
| 69 | 4761 |
| 70 | 4900 |
| 71 | 5041 |
| 72 | 5184 |
| 73 | 5329 |
| 74 | 5476 |
| 75 | 5625 |
| 76 | 5776 |
| 77 | 5929 |
| 78 | 6084 |
| 79 | 6241 |
| 80 | 6400 |
| 81 | 6561 |
| 82 | 6724 |
| 83 | 6889 |
| 84 | 7056 |
| 85 | 7225 |
| 86 | 7396 |
| 87 | 7569 |
| 88 | 7744 |
| 89 | 7921 |
| 90 | 8100 |
| 91 | 8281 |
| 92 | 8464 |
| 93 | 8649 |
| 94 | 8836 |
| 95 | 9025 |
| 96 | 9216 |
| 97 | 9409 |
| 98 | 9604 |
| 99 | 9801 |
| 100 | 10000 |
© Burada yayınlanan metinler kaynağı ve lisansı bildirilenler hariç hesabet.com'a ait özgün metinlerdir. Herhangi bir yerden alıntı değildir. Bu metinler derslerde kaynak olarak kullanılabilir ancak başka bir web sitesi, görsel veya yazılı ortamda yayınlanamaz.